Die Eintrittswahrscheinlichkeit bei Unsicherheit oder Ungewissheit ist nicht bekannt. Das bedeutet, dass keine Aussage darüber getroffen werden kann. Des Weiteren ist es unbefriedigend, weil wir nichts mehr wünschen als Sicherheit oder wenigstens konkrete Aussagen, die uns diese vorgaukeln. Aber das ist eben genau der Unterschied zwischen Unsicherheit und Risiko.
Beim Risiko sind die Eintrittswahrscheinlichkeiten bekannt. Bei einem fairen Münzwurf ist davon auszugehen, dass entweder Kopf oder Zahl fällt. Die Wahrscheinlichkeit für beide Fälle ist damit 50%. Dafür muss jedoch ausgeschlossen sein, dass die Münze auf dem Rand stehen bleiben kann. Also definieren wird für diesen unwahrscheinlichen Fall, dass erneut geworfen werden muss. Ansonsten sinkt die Eintrittswahrscheinlichkeit in beiden Fällen unter 50%, weil eben der Rand ebenfalls möglich ist.
An den Finanzmärkten ist nicht vorhersehbar, was passieren wird. Es lässt sich auch keine Eintrittswahrscheinlichkeit für bestimmte Kursveränderungen angeben. Denn die Vergangenheit zeigt eben nicht vollständig alle möglichen Ausgänge, sondern nur einen kleinen Teil derer. Das bedeutet, dass keine Aussage darüber möglich ist, wie tief die Kurse an einem Tag steigen oder fallen können und ebenso wenig, in welcher Kursspanne sie liegen könnten. Das ist unbefriedigend, aber leider nicht zu ändern.
Abschätzen der Eintrittswahrscheinlichkeit bei Unsicherheit
Dennoch wird versucht, Aussagen über die Eintrittswahrscheinlichkeit bei Ungewissheit treffen zu können. Vermutlich, weil es ein besseres Gefühl verspricht, als akzeptieren zu müssen, nichts zu wissen. Aber jegliche Aussagen betreffen eben nur die Erfahrungen der Vergangenheit! Schon der Haftungsausschluss sagt deutlich, dass Ergebnisse der Vergangenheit keiner Aussagen über die Zukunft ermöglichen und alles auch ganz anders kommen kann. Wei bei vielen Dingen, die nie vorkamen, bis sie zum ersten Mal passiert sind.
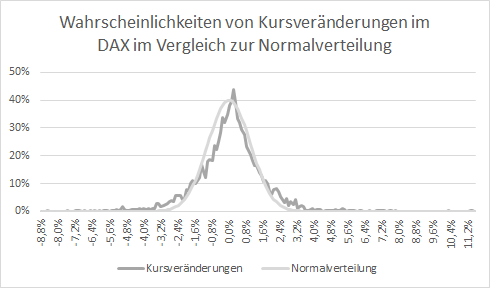
Obwohl wir wissen, dass es keine Aussage für die Zukunft erlaubt, werfen wir deshalb einen Blick auf die täglichen Kursveränderungen des DAX der letzten 20 Jahre. Zum Vergleich wird zusätzlich die Normalverteilung eingetragen, welche die zufällige Streuung von Werten darstellt. Interessant ist, dass den meisten finanzmathematischen Modellen die Annahme zugrunde liegt, Kursveränderungen wären normalverteilt.
Das ist durchaus verständlich, ähneln sich die eingetragenen Kurven doch sehr. Aber ähnlich ist eben nicht gleich. Nur, weil nichts Besseres verfügbar ist, um zu einem Ergebnis zu kommen, ist dieses noch lange nicht gut oder verwendbar. Denn die Annahme, dass beide Kurven gleich sind, beinhaltet gleich zwei Fehler. Zum einen ist die Normalverteilung eine Aussage zur Eintrittswahrscheinlichkeit zukünftiger, zufälliger Ergebnisse. Zufällig ist jedoch nicht ungewiss. Und die Kursveränderungen sind jedoch schlicht Ergebnisse der Vergangenheit, über deren Ursache wir nichts oder zumindest bei weitem nicht genug wissen. Also ein klarer Fall eines Äpfel-mit-Birnen-Vergleichs!
Kleine Fehler, große Wirkung
Zum anderen, und das ist offensichtlich, sind die Kurven eben nicht gleich. Daraus resultiert an gewissen Stellen ein Fehler, eben der Unterschied zwischen beiden Kurven. Dieser mag im Zentrum der Grafik noch akzeptabel sein, weil selbst der Faktor zwischen 20% und 40% nur 2 beträgt. Faktor 2 ist lediglich doppelt so hoch. An den Rändern ist der Fehler allerdings nicht mehr akzeptabel. Denn bspw. bei -3,2% ist der Faktor zwischen beiden Werten rund 100! Eine Kursrückgang um 3,2% war damit 100 mal wahrscheinlicher, als es die Normalverteilung in der Zukunft erwarten lassen würde.
Ganz am Rand der Grafik liegt der Faktor im Bereich einer Zahl mit 20 Nullen (im Negativen) und 25 Nullen (im Positiven). Im Vergleich dazu ist die Wahrscheinlichkeit im deutschen Lotto zu gewinnen mit 8 Nullen schon fast Sicherheit! (Ironie 😉 Dies ergibt sich daraus, dass die Zahlen so unglaublich klein sind und kleine absolute Abweichungen deshalb relativ groß sein können.
Das bedeutet, wenn die Finanzindustrie mit ihren Produkten ein Spiel konstruiert, unter der Annahme der Normalverteilung, sind die Ergebnisse nicht fair! Denn es ist wie eine Münze, die zwar in der Theorie mit gleicher Wahrscheinlichkeit Kopf oder Zahl zeigt, in der Praxis aber nicht. Natürlich werden noch Gebühren und Profite aufgeschlagen, die zu Lasten der Käufer / Dir gehen. Dadurch ändert sich jedoch nicht die grundsätzliche Betrachtung. Es sollte Dir daher darum gehen, Produkte zu finden, deren Verteilung zu Gunsten der Käufer / Dir verschoben ist.
Ist die Börse ein großes Kasino?
Ein weiteres Problem ist, dass ein Zeitraum von 20 Jahren bei rund 250 Börsentagen im Jahr nur rund 5.000 Kursveränderungen beinhaltet. Dies ist nicht viel und es wäre statistisch schon wesentlich besser, wenn wenigstens 50.000 oder noch besser 250.000 Werte zur Verfügung stünden. Dies wären jedoch 200 bzw. 1.000 Jahre Kursdaten, die erst im 22. bzw. 31. Jahrhundert (!) vorliegen werden. Nicht nur, dass die Verteilung nicht passt, die Datengrundlage ist auch noch mehr als dürftig.
Aktien sind Unternehmensbeteiligungen und Indizes wie der DAX sind Gruppen von Aktien. Selbst wenn es den Anschein hat, Kursbewegungen sind garantiert nicht zufällig. Schon gar nicht, nur weil es niemandem gelingt, diese Vorherzusagen. Dahinter liegt jedoch immer ein Wert und jeder Käufer oder Verkäufer hat eine Vorstellung davon, wie sich der Kurs in Zukunft entwickelt. Oder zumindest eine Präferenz, ob er die Aktie oder einen gewissen Gegenwert in Geld bevorzugt.
Die Börse ist also genau kein Kasino, weil im Kasino sehr präzise Regeln existieren und die Eintrittswahrscheinlichkeiten von Ergebnissen genau berechenbar oder zumindest abschätzbar sind. Trotzdem hängt es an der Börse und im Kasino mit Glück zusammen, ob Du gewinnst. Bzw. mit Pech, wenn Du verlierst. Wie soll es auch anders sein, wenn die Zukunft ungewiss ist?
Eintrittswahrscheinlichkeit bei Unsicherheit bleibt unbekannt
Zur Sicherheit möchte ich erneut erwähnen, dass diese Überlegungen zu Wahrscheinlichkeiten keine Grundlage haben. Sie versuchen lediglich den Fehler auszunutzen, der durch die Unterschiede zwischen der Normalverteilung und den historischen Erfahrungswerten von Kursveränderungen sichtbar ist. Diese Erfahrungswerte verändern sich jedoch mit jedem neuen Wert der hinzukommt!
Außerdem ist nicht im geringsten klar, wie groß der Zusammenhang mit der Zukunft sein wird. Die Zukunft kann komplett anders aussehen, was ein böses Erwachen zur Folge hat. Aber vielleicht sind die Ergebnisse auch perfekt normalverteilt – ich würde allerdings nicht darauf wetten (ernst). Denn die Eintrittswahrscheinlichkeit bei Unsicherheit ist nicht kalkulierbar!

